SOFEM: Field Computation and Raytracing in Lenses and Deflectors

This software package is supplied as an upgrade to the OPTICS and ABER-5 package.

SOFEM computes potential and field distributions in electrostatic and magnetic lenses and deflectors, using the second-order finite element method (SOFEM).  The program provides at least an order of magnitude greater accuracy than the first-order FEM for a given number of mesh-points.  As successively more mesh-points are used, the relative accuracy with respect to the first-order method becomes progressively greater.  The second-order method is also less sensitive to the distribution of mesh-points than the first-order method.  Since the field components are obtained to a high accuracy, the trajectories obtained with this software are very accurate, and can be used to estimate the lens aberrations directly from the raytrace.  (This is difficult to do very accurately with the first-order FEM.)

For electrostatic lenses, curved electrodes and dielectric materials can be handled easily.  For magnetic lens field analysis, there are three programs.  The first computes the magnetic scalar

potential distribution in the polepiece region assuming constant permeability polepieces.  The second computes the vector potential distribution in the magnetic circuit and coil windings, again assuming constant permeability.  The third program computes the vector potential in the magnetic circuit and coil windings, taking magnetic saturation into account, with numerically specified B-H curves, defined by the user.

Magnetic deflectors with toroidal or saddle coils can be handled, located inside rotationally symmetric magnetic circuits or wound on rotationally symmetric magnetic formers.  The program computes the first, third and fifth harmonic components of the deflection field.  Electrostatic multipole deflectors can

be handled.  To enable the field to be computed as a set of multipole harmonic compo-nents, the electrostatic poten-tial is assumed to vary linearly in the azimuthal direction in the azimuthal gaps between adjacent electrodes.  Again, the first, third and fifth harmo-nics of the deflection field are computed.

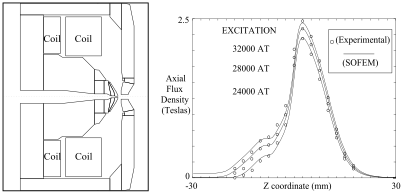
After computing the lens fields, direct ray-tracing in the rotationally symmetric fields is performed using a Runge-Kutta formula.  The field components at each point on the trajectory are obtained by interpolation between 5 second-order finite elements.

Facilities are provided for plotting equipotentials, magnetic flux lines, axial focusing and deflection functions, and plots of the electron or ion trajectories from the direct ray-tracing.

If you are interested in the SOFEM package, please contact us at info@electronoptica.com.

Highly saturated magnetic lens.      Axial flux density in gap, exp. vs. theory.

Toroidal deflector inside a magnetic        Computed deflection field harmonics for the lens.                                                          toroidal deflector.